Teoria dos Grafos

O que é um grafo

Um grafo nada mais é do que um conjunto de vértices conectados por arestas, cuja notação é G = (V,E). Os grafos são uma estrutura de dados muito importante para a ciência da computação, uma vez que com eles é possível resolver uma grande variedade de problemas computacionais. Com eles é possível representar uma rede de relações entre componentes, como usuários em redes sociais ou até fluxos de dependências em programas de computador. Vale mencionar que importantes aplicações da atualidade como: Google Maps, Git, redes sociais e Compiladores utilizam amplamente grafos e seus algoritmos.

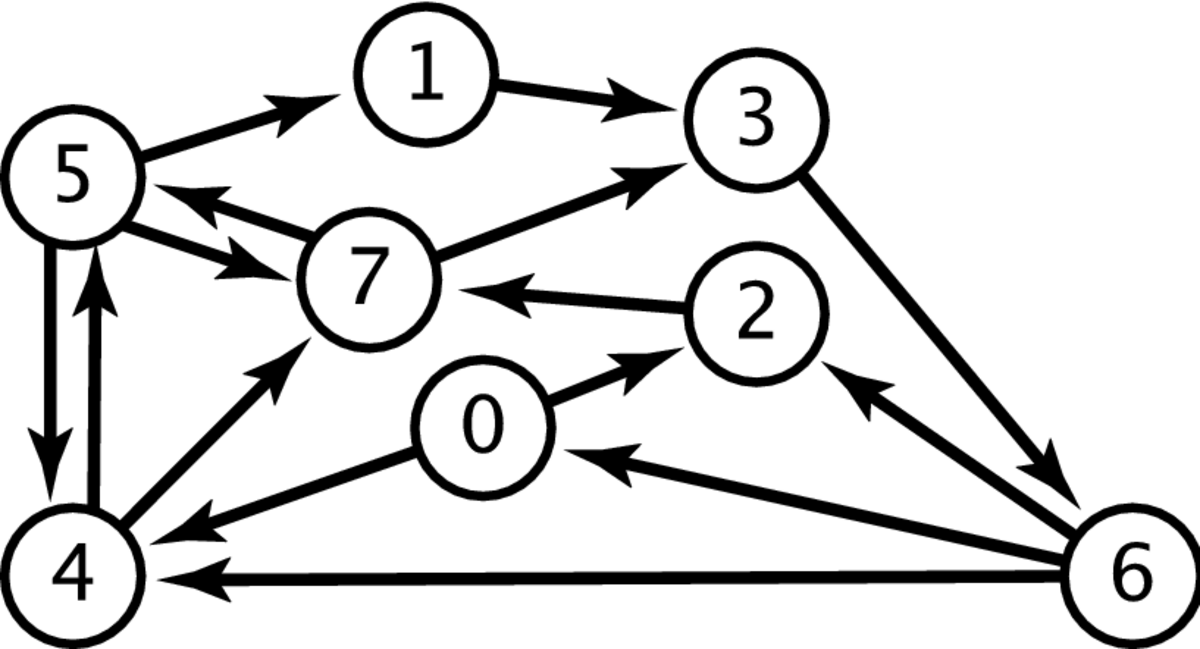
O Grafo acima possui os vértices (0, 1, 2, 3, 4, 5, 6, 7) e as arestas ( (1 - 3), (3 - 6), (6 - 2), (6 - 0), (6 - 4), (4 - 7), (4 - 5), (0 - 2), (0 - 4), (7 - 5) , (7 - 3), (5 - 1), (5 - 7), (5 - 4) ).

Grafos direcionados

O grafo representado na imagem 1 é um exemplo de grafo direcionado. Em um grafo direcionado as arestas possuem uma direção, ou seja na aresta (A - B) é possível ir do vértice A para o B, mas não do vértice B para o A. Vale mencionar que, se é possível ir de um vértice X para um vértice Y, se diz que Y é adjacente a X.

Grafos não direcionados

Em um grafo não direcionado, as arestas não possuem sentido, ou seja, a mesma aresta (A - B) em um grafo não direcionado nos diz que é possível ir tanto de A para B, quanto de B para A.

Peso

Nós também podemos associar pesos as arestas. Os pesos representam o quão custoso é ir percorrer uma aresta. No grafo não direcionado representado na imagem acima possui pesos. Os pesos podem representar uma métrica qualquer. Suponhamos que o peso no grafo acima, o peso representa a distância em mettros entre 2 vértices. Sendo assim, se você for do vértice 3 para o 0 (ou do 0 para o 3), você percorerá 7 metros.

Caminhos e Ciclos

Para fechar, vamos falar sobre caminho e ciclo. Um caminho é uma sequência ordenada de arestas que possibilitam, a partir de um vértice a, alcançar um vértice b. Por exemplo, o caminho entre os vértices 1 e 4 no segundo grafo é (1 - 3 - 4) ou (1 - 0 - 4). O ciclos, por sua vez, são caminhos onde a origem e o destino são o mesmo vértice.

Conclusão

Esse artigo nada mais é do que uma breve introdução a teoria dos grafos, que é um vasto campo de estudo da ciência da computação. Se você quer melhorar sua lógica de programação e a sua capacidade de resolver problemas vale a pena investir um pouco no assunto de grafo. Mais para frente estarei lançando mais artigos sobre conceitos básicos de grafos e seus algoritmos elementares.

Se você quiser saber como que os grafos são implementados na prática, da uma olhada na biblioteca que eu estou fazendo para manipular grafos na linguagem C#.

link para o reprositório no git - dá uma estrelhinha lá se você puder :)

Referências

Algoritmos Teoria e Prática Introduction to Graph Theory: A Computer Science Perspective Grafos: Conceitos, algoritmos e aplicações Aula de AEDS - 2020-10-19 - 13h30 - Grafos (01/02)