Como os Supercomputadores Simulam o Mundo Real: Difusão de Calor em Paralelo!

Nota do Autor:

"Olá Pessoal, eu aqui de volta com um assunto sobre supercomputação! Minha relação com essa área é cheia de ida de voltas. Já trabalhei na área em uma empresa de supercomputação em 2022 e em 2024. Lá aprendi bastante sobre conceitos da área com pessoas com anos de atuação de forma profissional e acadêmica. Foi amor a primeira vista, lembro até hoje que parecia que eu tinha descoberto uma área que se encaixava perfeitamente em teoria e prática. Comecei estudando computação paralela, depois disso arquitetura de computadores e outros assutos que são extremamente necessário para área como sistemas operacionais e redes. Sou muito grato a todos que puderam me ensinar sobre. Como disse em outros artigos que escrevi, faz um tempo que não codifico nada e minha parte técnica hoje serve para resolver problemas pontuais, pois minha atuação é na área de gestão e estratégia. Mas meu coração está aqui: na computação, no código."

Introdução

Você já se perguntou como o calor se espalha em um objeto? Como a temperatura em uma chapa metálica se distribui ao longo do tempo? Esses fenômenos são essenciais em engenharia, climatologia e até mesmo na medicina.

Mas como cientistas e engenheiros conseguem prever isso? A resposta está na simulação computacional, que permite modelar o comportamento do calor e prever sua propagação. No entanto, simular esses fenômenos pode ser computacionalmente caro, exigindo recursos que vão além de um simples computador doméstico.

Neste artigo, vamos explorar:

• Como funciona a difusão de calor.
• Como podemos programar um computador para simular esse fenômeno.
• Como utilizamos computação paralela para acelerar a simulação.
• Como usar MPI (Message Passing Interface) para dividir o problema entre vários processadores.

O que é a Difusão de Calor?

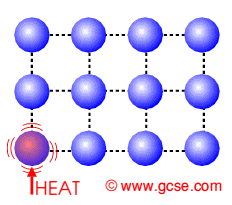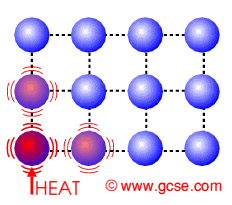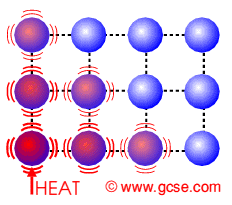
A difusão de calor é um processo físico onde a temperatura se espalha de regiões mais quentes para mais frias. Esse comportamento pode ser modelado matematicamente pela Equação do Calor:

$$ \frac{\partial u}{\partial t} = \alpha \left( \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} \right) $$

Onde:

• ( u(x,y,t) ) é a temperatura em um ponto do espaço ao longo do tempo.
• ( \alpha ) é o coeficiente de difusividade térmica, que depende do material.
• ( x, y ) são as coordenadas espaciais.
• ( t ) representa o tempo.

Esse modelo é útil para prever a distribuição de calor em objetos sólidos, como peças metálicas, placas de circuitos eletrônicos e até o manto terrestre.

Computação Paralela: Por que Precisamos?

Se quisermos simular a difusão de calor em uma pequena chapa metálica com poucos pontos, um computador comum pode resolver o problema rapidamente. Mas e se quisermos simular um grande pedaço de metal, um reator nuclear ou a crosta terrestre?

Conforme aumentamos o tamanho da simulação, a quantidade de cálculos cresce exponencialmente. Um notebook pode levar dias ou até semanas para resolver esses problemas.

A solução para esse problema é a computação paralela, onde distribuímos os cálculos entre vários processadores. Utilizando MPI (Message Passing Interface), podemos dividir a matriz da simulação entre múltiplos núcleos, permitindo que vários cálculos aconteçam simultaneamente.

MPI (Message Passing Interface) e um pouco de paralelismo:

Paralelismo é uma técnica utilizada na computação para realizar múltiplas operações simultaneamente. Ao invés de processar uma tarefa de forma sequencial — uma instrução após a outra — o paralelismo divide a tarefa em várias partes menores, que podem ser executadas ao mesmo tempo por diferentes unidades de processamento. Isso acelera o tempo total de execução e otimiza o uso dos recursos disponíveis.

MPI (Message Passing Interface) é um padrão para comunicação entre processos, especialmente desenvolvido para computação paralela distribuída. Ele é amplamente utilizado em ambientes onde múltiplos computadores (ou nós) trabalham juntos para resolver um problema grande e complexo. O MPI implementa paralelismo, onde diferentes partes de uma tarefa é processada por diferentes nós em um cluster. Os processos podem estabelecer uma comunicação entre si de forma que contribua para o progresso do problema calculado. Como não há compartilhamento de memória entre os processos, é possível usar o MPI para escalar para milhares de nós com rede. Abaixo um exemplo de comunicação entre processos usando o MPI_Send e o MPI_Recv:

MPI_Send(&grid[1][0], cols, MPI_DOUBLE, rank - 1, 0, MPI_COMM_WORLD);
MPI_Recv(&grid[0][0], cols, MPI_DOUBLE, rank - 1, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);

Aqui, um processador envia sua primeira linha interna para o vizinho de cima e recebe a borda inferior do vizinho de cima. Isso garante que a simulação continue sem inconsistências.

O paralelismo aumenta significativamente a eficiência e velocidade de processamento. O MPI se aproveita desse conceito, permitindo que processos independentes em sistemas distribuídos comuniquem-se de forma eficaz. Juntos, eles são fundamentais para resolver problemas complexos em áreas como simulações científicas, análise de dados em larga escala e aprendizado de máquina.

Como Funciona o Código da Simulação?

A simulação foi implementada em C++ com MPI, onde:
1️ Criamos uma grade 2D representando o material usando estrutura de dados da linguagem.
2️⃣ Definimos as condições iniciais, com uma borda aquecida em condições que podemos alterar.
3️⃣ Utilizamos um método iterativo para calcular a temperatura de cada ponto ao longo do tempo.
4️⃣ Dividimos a matriz entre diferentes processadores, onde cada um calcula uma parte.
5️⃣ No final, juntamos os resultados em um único processador e salvamos os dados.

Passo 1: Inicialização da Grade

Cada ponto da matriz começa com uma temperatura inicial, sendo que a borda superior da grade está aquecida (simulando uma fonte de calor).

void initialize_grid(std::vector<std::vector<double>> &grid, int rank, int size) {
    for (int i = 0; i < grid.size(); ++i) {
        for (int j = 0; j < grid[0].size(); ++j) {
            if (rank == 0 && i == 0) {
                grid[i][j] = 100.0; // Linha quente no topo
            } else {
                grid[i][j] = 0.0;
            }
        }
    }
}

Passo 2: Atualização da Temperatura

Usamos o método das diferenças finitas para calcular a temperatura em cada ponto da matriz:

void update_grid(std::vector<std::vector<double>> &current, std::vector<std::vector<double>> &next) {
    for (int i = 1; i < current.size() - 1; ++i) {
        for (int j = 1; j < current[0].size() - 1; ++j) {
            next[i][j] = current[i][j] +
                         ALPHA * (current[i - 1][j] + current[i + 1][j] +
                                  current[i][j - 1] + current[i][j + 1] - 4 * current[i][j]);
        }
    }
}

Passo 3: Rodando em paralelo

Agora utilizamos do paralelismo para poder trabalhar de maneira eficiente com os calculos: usando o MPI e funções como Rank com o intuito de enumerar os processos e Size para obter a quantidade de processos em execução:

int main(int argc, char **argv) {
    MPI_Init(&argc, &argv);

    int rank, size;
    MPI_Comm_rank(MPI_COMM_WORLD, &rank);
    MPI_Comm_size(MPI_COMM_WORLD, &size);

    // Divisão das linhas entre processos
    int local_rows = GRID_SIZE / size;
    std::vector<std::vector<double>> current_grid(local_rows + 2, std::vector<double>(GRID_SIZE, 0.0));
    std::vector<std::vector<double>> next_grid = current_grid;

    initialize_grid(current_grid, rank, size);

    for (int t = 0; t < TIME_STEPS; ++t) {
        update_grid(current_grid, next_grid);
        current_grid.swap(next_grid);

        // Comunicação entre processos
        if (rank > 0) {
            MPI_Send(&current_grid[1][0], GRID_SIZE, MPI_DOUBLE, rank - 1, 0, MPI_COMM_WORLD);
            MPI_Recv(&current_grid[0][0], GRID_SIZE, MPI_DOUBLE, rank - 1, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
        }
        if (rank < size - 1) {
            MPI_Recv(&current_grid[local_rows + 1][0], GRID_SIZE, MPI_DOUBLE, rank + 1, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
            MPI_Send(&current_grid[local_rows][0], GRID_SIZE, MPI_DOUBLE, rank + 1, 0, MPI_COMM_WORLD);
        }
    }

Passo 4: Agregação final

A grade(grid) de temperatura final é coletada e reconstruída pelo processo mestre.

 if (rank == 0) {
        std::vector<std::vector<double>> full_grid(GRID_SIZE, std::vector<double>(GRID_SIZE, 0.0));
        for (int i = 1; i <= local_rows; ++i) {
            full_grid[i - 1] = current_grid[i];
        }
        for (int p = 1; p < size; ++p) {
            MPI_Recv(&full_grid[p * local_rows][0], local_rows * GRID_SIZE, MPI_DOUBLE, p, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
        }
        save_grid_to_file(full_grid, rank); // Salva a grade completa em arquivo
        print_grid(full_grid, rank);       // Opcional: Imprime a grade no terminal
    } else {
        MPI_Send(&current_grid[1][0], local_rows * GRID_SIZE, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD);
    }

    MPI_Finalize();
    return 0;
}

Compilação

Para compilar o código, use o seguinte comando:

mpicxx -o heat_simulation heat_simulation.cpp

Execução

Execute o programa com mpirun, especificando o número de processos:

mpirun -np 4 ./heat_simulation

ou

mpirun --oversubscribe -np 4 ./heat_simulation

Resultados

• O programa salvará a grade de temperatura final em output_grid.txt.
• Se habilitado, o programa também imprimirá a grade no terminal

Conclusão

Bom, eu queria me aprofundar em detalhes linha por linha e explicar cada função. Mas para não decepcionar vou deixar o código completo abaixo. A supercomputação é uma área muito, mas muito legal. Eu diria que é para quem quer ciência da computação aplicada para resolução de problemas científicos esse é o caminho. No futuro predento trazer artigos que sejam direcionados a treinamento de modelos de aprendizado profundo usando processos da supercomputação.

Link para o Github: https://github.com/samsepiol1/HeatSimulation-HPC

Link para o Linkedin: https://www.linkedin.com/in/lucas-matheus-3809aa121/