Como a Tranformada Rápida de Fourier (FFT) mudou o mundo!

A Transformada Rápida de Fourier é basicamente um algoritmo para se calcular a Transformada de Fourier Discreta (DFT) de forma muito mais rápida. Em primeiro lugar, precisamos entender o que significa a transformada de Fourier: A transformada de Fourier é uma função matemática que decompõe uma forma de onda, que é uma função do tempo, nas frequências que a compõem. O resultado produzido pela transformada de Fourier é uma função valorada complexa de frequência. O valor absoluto da transformada de Fourier representa o valor da frequência presente na função original e seu argumento complexo representa o deslocamento de fase da senoidal básica naquela frequência.[1] Ficou complicado de entender? calma! irei vou dar um exemplo a seguir. Imagine que você trabalhe com a parte elétrica de uma indústria manuseando correntes elétricas alternadas. Certo dia seu patrão pede para que você programe um microcontrolador para produzir correntes com formato de ondas quadradas (ou aproximações disso). Como você trabalha com correntes senoidas, você precisa achar um jeito de combinar os senos e cossenos para, de alguma forma, fazer uma onda quadrada. É nessa parte que entra a transformada de Fourier. Ela consegue decompor uma função quadrada em termos de senos e cossenos - calibrando quais frequências devem ser mais ou menos adicionadas em senos e cossenos para se produzir a função de onda quadrada.

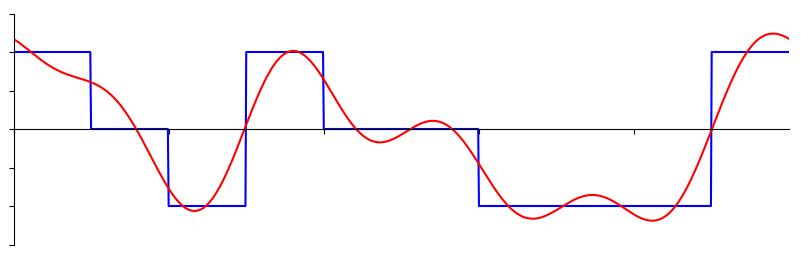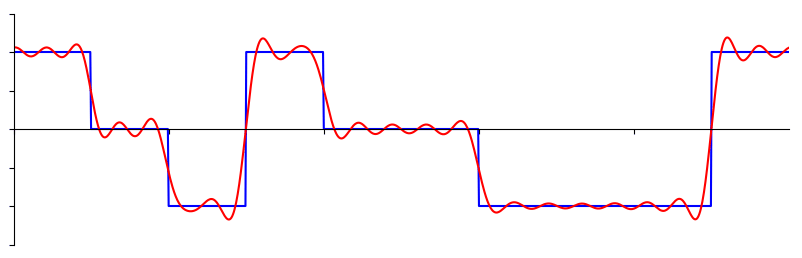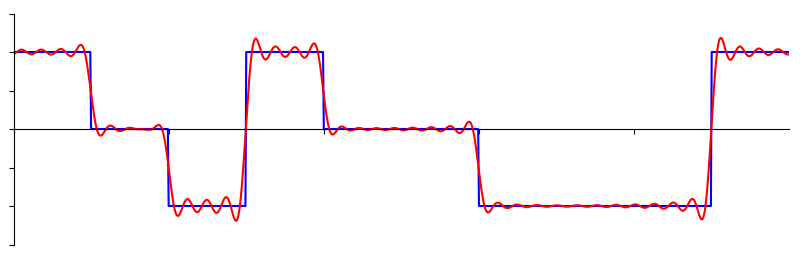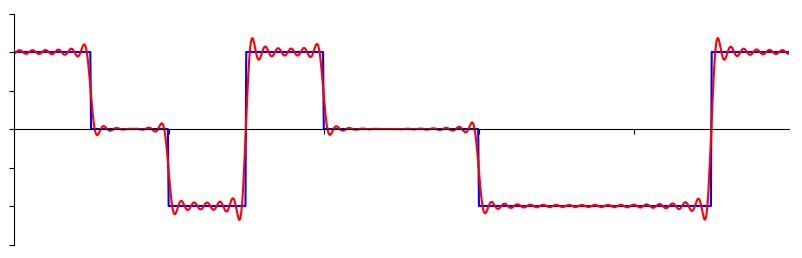
A transformada de Fourier também é chamada de generalização da série de Fourier. Este termo também pode ser aplicado tanto à representação no domínio da frequência quanto à função matemática usada. A transformada de Fourier ajuda a estender a série de Fourier para funções não periódicas, o que permite visualizar qualquer função como uma soma de senoides simples.[1].

Nesse sentido, podemos ver que uma ampla gama de funções podem ser estudadas com base em sua representação na frequência! Isso é incrível em muitos sentidos: imagine que anteriormente teríamos de analisar as funções em somente um domínio (geralmente envolvendo o tempo) e, com a descoberta da transformada de Fourier, temos a possibilidade de analisar essa mesma função no domínio da frequência. Desde a frequência dos níveis de energia dos átomos até o brilho de galáxias inteiras podem ser modeladas usando Fourier. Aliás, veja abaixo uma aplicação de Fourier:

As frequências de luz emitidas por estrelas possuem uma íntima relação com os materiais que estão presentes nessa mesma estrela. O telescópio James Webb deixou issou muito claro com essas imagens. Magnífico!

Mas qual a diferença da Transformada de Fourier Discreta para a Transformada Rápida de Fourier?

Veja bem ao seu redor: Nosso mundo está se tornando cada vez mais digitalizado. As imagens que você vê em um aparelho digital estão digitalizadas e quantizadas provavelmente em valores que vão de 0 até 255 para o padrão RGB. Com o advento da com o advento da computação, muitas coisas tiveram de ser convertidas de analógico para digital. Esse é o caso de imagens, mensagens, comunicações telefônicas e muitas outras coisas. Conforme o nível da eletrônica aumentava, a necessidade para se realizar transformações envolvendo o domínio da frequência também aumentava.

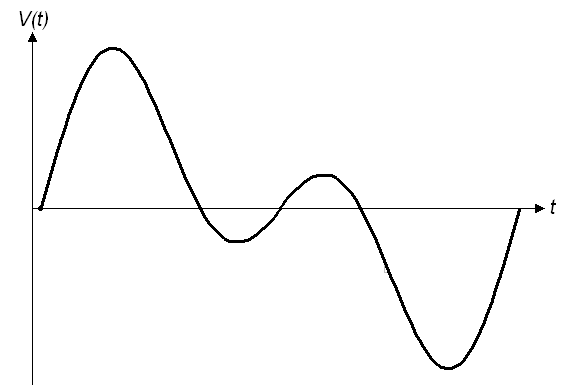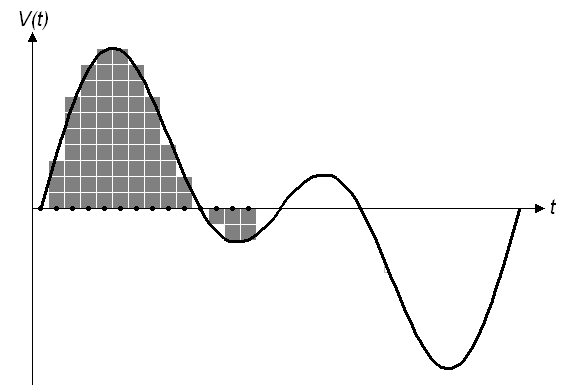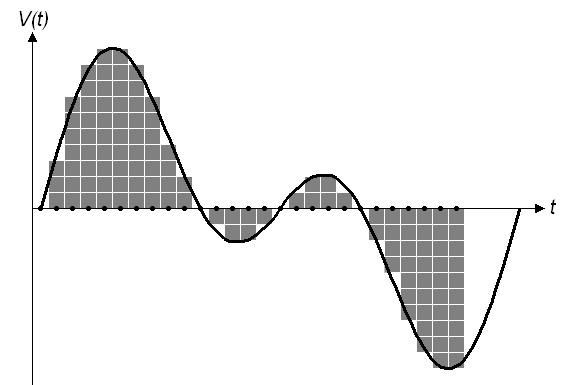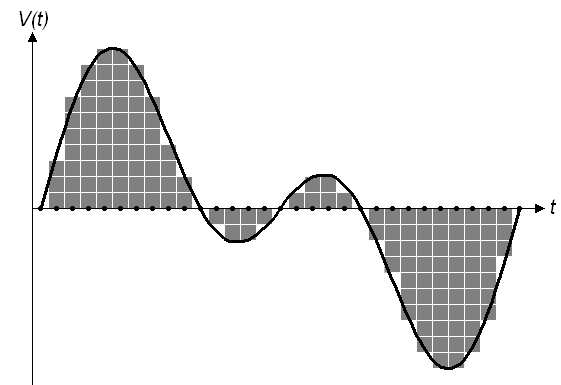
Nesse contexto surgiu a ideia de aplicar a Transformada de Fourier Discreta(DFT). Ela possui a mesma finalidade da Transformada de Fourier - Na medida em que a transformada pega uma função e "cospe" outra função, a DTF pega pontos e "cospe" outros pontos. Vou dar um exemplo: A voz humana. Quando você realiza uma gravação sua, você está armazenando valores discretizados e quantificados de sua voz em amplitude e intensidade sonora. A título de curiosidade, geralmente os aparelhos que realizam essa gravações possuem frequências de amostragem maiores que 40000 amostras/segundo para suprirem a capacidade de audição do ouvido humano (20 até 20kHz). Para analisar a frequência da sua voz, aplicamos a DTF nas amostras de áudio que obtemos e voilà! Teremos um diagrama com o espectro da voz!

Acontece que nem tudo é perfeito e a DFT é um exemplo disso. Computacionalmente falando, aplicar ela em uma grande quantidade de dados é o terror de qualquer computador. Irei explicar o porquê disso ocorrer logo abaixo.

DFT dá medo 😱😱

Se você já estudou álgebra linear, sabe que os matemáticos adoram matrizes. Matrizes são otimas para transformações lineares e cairam como uma luva para aplicações da DFT.

E a razão era a sua praticidade: pegue os pontos que você deseja saber sua DFT (x), multiplique pela matriz transformação (S*) e você obterá a DFT desses pontos (X). Bem simples, não é?

Por algum tempo essa foi a solução utilizada para se realizar a Transformada Discreta, mas o reinado dessa abordagem não iria demorar muito, pois havia um grande problema crucial: o custo de processamento.

Analise bem 🤔. Para matrizes pequenas podemos fazer sem grandes problemas a DFT, mas, conforme o tamanho dos dados que você deseja saber aumenta (x), a matriz transformação também aumenta (S*). Além disso, a situação é uma das piores possíveis, pois ela aumenta quadraticamente (😱😱)!!

Abaixo temos uma matriz transformação para 4 pontos:

e agora para 8 pontos:

Viu como da medo?!? Agora imagina que em um segundo o seu aparelho celular registrou cerca de 44 mil amostras. Teoricamente, a matriz transformação disso seria 193.600.000! Seria um absurdo de custo computacional. Em dois minutos de conversa minutos de conversa, você teria 2,3232e10 elementos para realizar uma operação. Em resumo, não há como avançar.

A FFT volta das cinzas

Este método (e a ideia geral de uma FFT) foi popularizado por uma publicação de Cooley e Tukey em 1965, mas foi descoberto mais tarde que esses dois autores reinventaram independentemente um algoritmo conhecido por Carl Friedrich Gauss por volta de 1805(e subsequentemente redescoberto várias vezes em formas limitadas). Você não leu errado. Se esse senhor (da imagem abaixo) tivesse publicado o seu conhecimento, provavelmente estaríamos uns 60 anos no futuro.

A FFT é elegante e, de certa forma, simples. Nesse momento, irei me ater mais ao algoritmo Radix-2. O algoritmo possui uma vantagem sobre a DFT pois "quebra" uma grande quantidade de dados em partes menores. Imagine que você tenha que fazer uma DFT de um ventor de 8 números. Você prefere fazer uma multiplicação com 64 itens ou multiplicar duas matrizes com 16 itens cada? A reposta é óbvia. Devido a esse motivo a FFT é chamada de Rápida! Ela consegue fazer com que um vetor de 8 números seja quebrado em dois vetores com 4 números. Esses dois vetores de 4 números podem ser quebrados em quatro vetores com 2 números cada. Note que o número de operações que temos de realizar caiu expressivamente! de 64 operações, ficamos com apenas 16 operações!

Essencialmente, a FFT possui um custo computacional de (N Log(N)) enquanto a DFT de (N²).

E essa mudança mudou todo o jogo.

Os efeitos da FFT

Sabe o 5G - a nova geração de internet que somente de investimentos em infraestrutura está com o valor previsto para 2 trilhões e 7 bilhões de dólares? Eu vou te contar um segredo sobre essa nova tecnologia 🤫

Essa tecnologia usa uma modulação de dados que está intrinsecamente relacionada com a FFT. O nome dessa modulação é OFDM/OFDMA (Orthogonal Frequency Division Multiplexing / Multiple Access) e ela utiliza sub-portadoras na frequência para a transmissão de informações. Para se moldar essa relação na frequência com os dados, é usado uma técnica da FFT inversa (IFFT). Sobre essa técnica, ela está presente no Wireless e na Discrete Multi-tone Transmission (DMT).

Além de estar amplamente presente no ramo de Telecomunicações, a FFT é usada diversas vezes para análises musicais, medição de temperatura, análise de exoplanetas, comportamento sísmico e etc.

Se você, assim como eu, achou interessante esse tópico, saiba que existe uma biblioteca em Python perfeita para essa usabilidade. Provavelmente você conhece a Numpy. NumPy é uma biblioteca para a linguagem de programação Python, adicionando suporte para matrizes e matrizes grandes e multidimensionais, juntamente com uma grande coleção de funções matemáticas de alto nível para operar nessas matrizes. Para acessar as usabilidades da fft, importe o arquivo

import numpy.fft

e desse modo você poderá usar diversas operações. Caso você programe em Rust, há uma biblioteca chamada RustFFT. RustFFT é uma biblioteca FFT acelerada por SIMD de alto desempenho escrita em puro Rust. Ele pode calcular FFTs de qualquer tamanho, incluindo tamanhos de números primos, em tempo O(nlogn).

e a sua importação se dá por:

// Perform a forward FFT of size 1234
use rustfft::{FftPlanner, num_complex::Complex};

CURIOSIDADE: Transformada de Fourier Quântica?

Sim, é possível realizar a transformada quântica de Fourier (QFT)

Irei deixar o link nas referências bibliográficas [3]. Mas é possível usar as bibliotecas abaixo para fazer a simulação:

import numpy as np
from numpy import pi
# importing Qiskit
from qiskit import QuantumCircuit, transpile, assemble, Aer, IBMQ
from qiskit.providers.ibmq import least_busy
from qiskit.tools.monitor import job_monitor
from qiskit.visualization import plot_histogram, plot_bloch_multivector

e é isso pessoal! espero que tenham gostado. Até a próxima!

REFERÊNCIAS BIBLIOGRÁFICAS

[1] - Fourier Transform .Disponível em: https://www.techopedia.com/definition/7292/fourier-transform. Acesso em 1 de dezembro de 2022.

[2] - Matrix DFT. Disponível em: https://en.m.wikipedia.org/wiki/DFT_matrix. Acesso em 1 de dezembro de 2022.

[3] - Transformada Quântica de Fourier. Disponível em:https://qiskit.org/textbook/ch-algorithms/quantum-fourier-transform.html. Acesso em 2 de dezembro de 2022.